Finance Application
If I contribute the maximum yearly amount to my IRA every year, how much will I have when I am 65 and would like to retire (40 years from now)? The maximum yearly contribution amount to an IRA is $5,000, and the interest rate is about 7% compounding continuously.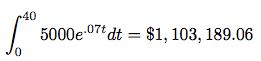
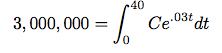
C = $38,791
. Wow!! This is what I would have to contribute yearly to that savings account to end up with $3,000,000 in my savings account when I retire. (Which is rather unrealistic on a math teacher's salary. I'll just have to stick with the $1,103,189.06 in my IRA when I retire!)Statistics Applications
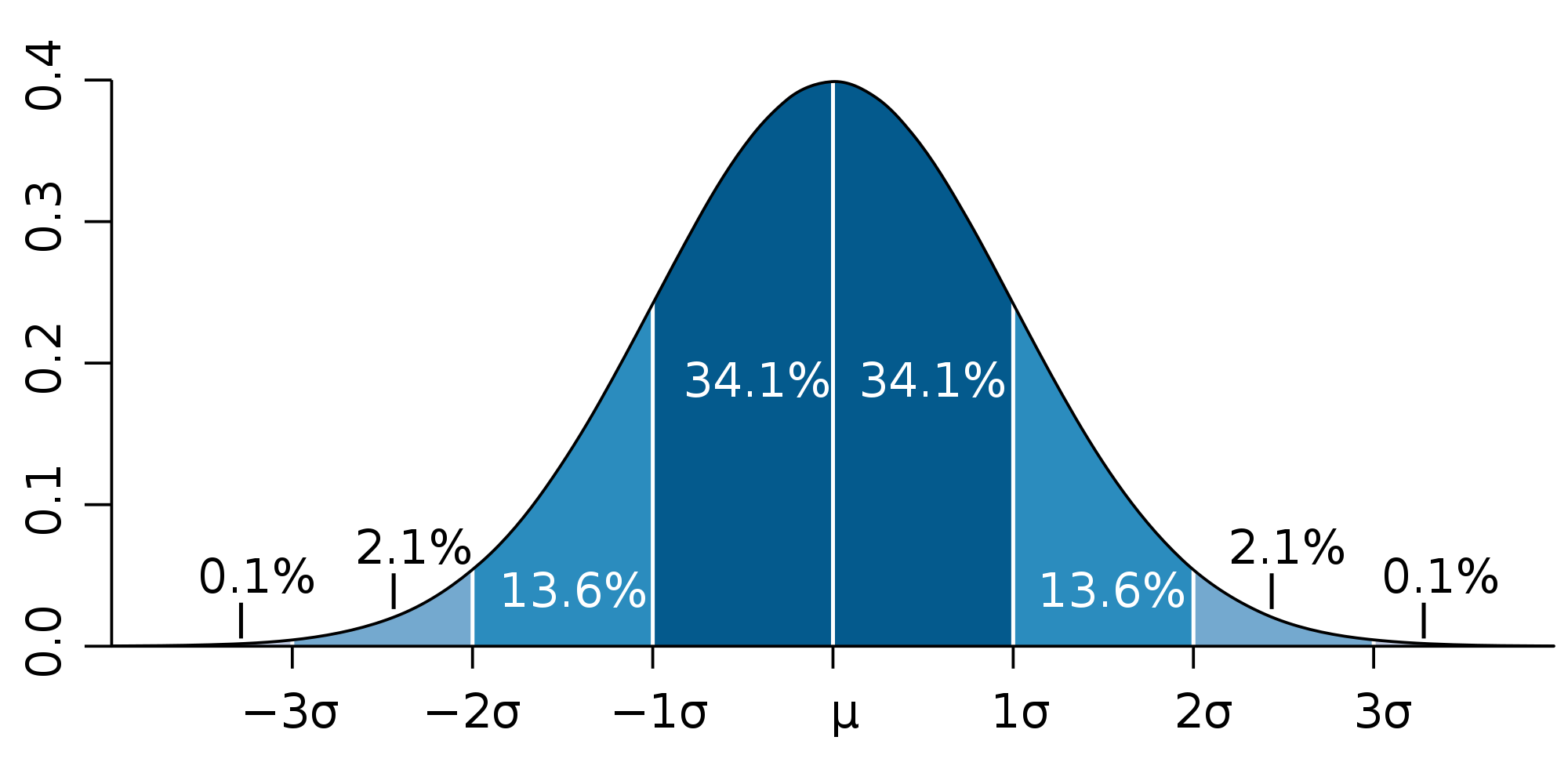 The Normal Curve is probably the most well-known and useful curves in statistics. Probability is computed by
finding the area under the curve for a certain interval -- what we call integration.
The Normal Curve is probably the most well-known and useful curves in statistics. Probability is computed by
finding the area under the curve for a certain interval -- what we call integration.
Another application of integration to statistics is the ability to compute the average y-value of a function over an interval (not to be confused with the mean or expected value of a PDF function, although integration is used for that as well.)
The lifetime of a battery is a uniform random variable defined on the domain [30,50]. Find the probability that a battery lasts longer than 35 hours.

So, by integrating, we computed that the probability of a battery lasting longer than 35 hours is .75.
(Goldstein, 2014, p.562)
Physics Applications
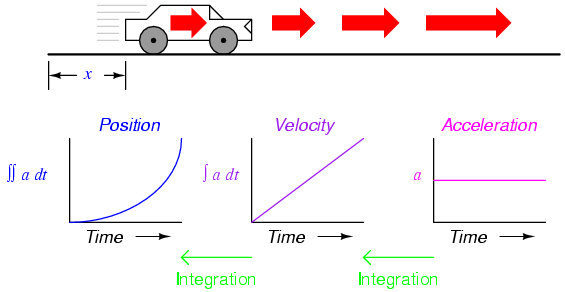 Integration and derivation is used EVERYWHERE in physics. A common use for integration and derivation in calculus
and physics is the relationship between the position, velocity, and acceleration of an object in motion.
Integration and derivation is used EVERYWHERE in physics. A common use for integration and derivation in calculus
and physics is the relationship between the position, velocity, and acceleration of an object in motion.
Another application is computing the work done by a pump:
How much work does it take to empty the tank by pumping the water back to ground level once the tank is full?
Before we find the work done, there are a couple of things we will need to know:
1. Work = Force x Distance
2. Force = Weight
3. Weight = Volume x Weight per unit

(Hass et. al., 2007, p. 434)